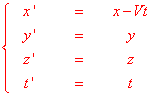TRASFORMAZIONI GALILEIANE
Il principio di relatività galileiana afferma l'assoluta equivalenza fisica di tutti i sistemi di riferimento inerziali: nessun esperimento eseguito all'interno di un dato sistema di riferimento può evidenziare il moto rettilineo ed uniforme dello stesso sistema, o, in altre parole, le leggi fisiche scoperte da sperimentatori che lavorino in laboratori in moto relativo rettilineo ed uniforme devono avere la stessa forma.Si tratta ora di ricavare le formule che legano le coordinate spazio temporali di uno stesso evento visto da due diversi riferimenti e di provare che le leggi della fisica sono invarianti, nella forma, al passaggio da un riferimento all'altro: si tratta cioè di tradurre in formule il contenuto di questo principio.
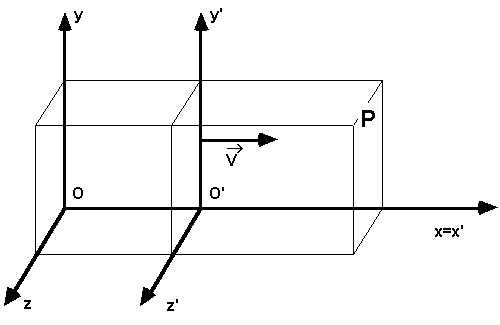
Si considerino due riferimenti, S ed S', di cui S' mobile, rispetto ad S, di moto rettilineo ed uniforme, con velocità V. Si supponga che gli osservatori solidali ad S e S' siano dotati di due orologi per la misura dei tempi, preventivamente sincronizzati in modo che, per esempio, quando O coincide con O' entrambi gli orologi segnino zero. Non è restrittivo prendere, come noi faremo, gli assi x dei due riferimenti sovrapposti, in modo che V sia parallela allo stesso asse x. Si consideri un certo evento fisico che avviene in un punto P con coordinate (x,y,z) e (x', y',z') rispetto a S e S' rispettivamente, e negli istanti t e t' misurati dai due osservatori. Tenendo conto che OO' = Vt e che sembra ovvio supporre t' = t, dalla figura qui sopra segue subito che valgono le cosiddette:
